11.2.1完全抗剪连接组合梁的抗弯强度应按下列规定计算:
1、正弯矩作用区段:
1)塑性中和轴在混凝土翼板内(图11.2.1-1),即Af≤behc1fc时:
M≤bexfcy
(11.2.1-1)
x=Af/(befc)
(11.2.1-2)
式中 M——正弯矩设计值;
A——钢梁的截面面积;
x——混凝土翼板受压区高度;工
y——钢梁截面应力的合力至混凝土受压区截面应力的合カ间的距离;
fc——混凝土抗压强度设计值。
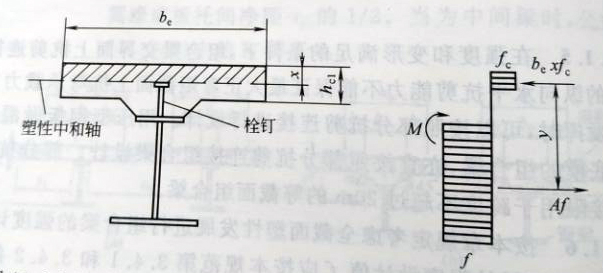
图11.2.1-1塑性中和轴在混凝土翼板内时的组合梁截面及应力图形
2)塑性中和轴在钢梁截面内(图11.2.1-2),即Af> behc1fc时:
M≤ behc1fcy1+Acfy2
(11.2.1-3)
Ac=0. 5(A-behc1fc/f)
(11.2.1-4)
式中Ac——钢梁受压区截面面积;
y1——钢梁受拉区截面形心至混凝土翼板受压区截面形心的距离;
y2——钢梁受拉区截面形心至钢梁受压区截面形心的距离。
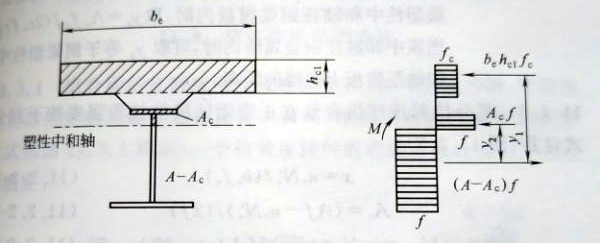
图11.2.1-2塑性中和轴在钢梁内时的组合梁截面及应力图形
2负弯矩作用区段(图11.2.1-3):
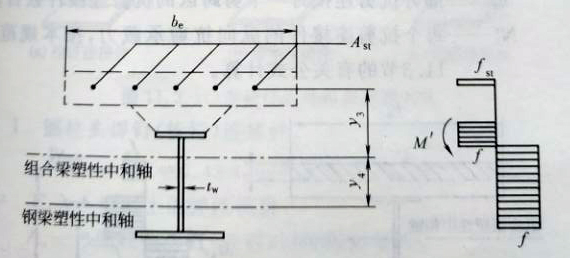
图11.2.1-3负弯矩作用时组合梁截面及应力图形
M’≤Ms+Astfst(y3+y4/2)(11.2.1-5)
Ms=(S1+S2)f
(11.2.1-6)
式中M’——负弯矩设计值;
S1、S2——钢梁塑性中和轴(平分钢梁截面积的轴线)以上和以下截面对该轴的面积矩;
Ast——负弯矩区混凝士翼板有效宽度范围内的纵向钢筋截面面积;
fst——钢筋抗拉强度设计值;
y3——纵向钢筋截面形心至组合梁塑性中和轴的距离;
y4——组合梁塑性中和轴至钢梁塑性中和轴的距离。当组合梁塑性中和轴在钢梁腹板内时,取y4=Astfst(2twf);
当该中和轴在钢梁翼缘内时,可取y4等于钢梁塑性中和轴至腹板上边缘的距离。
1.1.2部分抗剪连接组合梁在正弯矩区段的抗弯强度按下列公式计算(图11.2.2):
x=nrNcv /(befc)
(11.2.2-1)
Ac=(Af-nrNcv)/(2f)
(11.2.2-2)
Mu,r=nrNcvy1 +0.5(Af-nrNcv)y2
(11.2.2-3)
式中Mu,r——部分抗剪连接时组合梁截面抗弯承载力;
nr——部分抗剪连接时一个剪跨区的抗剪连接件数目;
Ncv——每个抗剪连接件的纵向抗剪承载力,按本规范第11.3节的有关公式计算。

图11.2.2部分抗剪连接组合梁计算简图。
部分抗剪连接组合梁在负弯矩作用区段的抗弯强度则按nrNcv和Astfst两者中的较小值计算。
11.2.3组合梁截面上的全部剪力,假定仅由钢梁腹板承受,应按
本规范公式(9.2.2)进行计算。
11.2.4用塑性设计法计算组合梁强度时,在下列部位可不考虑弯矩与剪力的相互影响:
1 受正弯矩的组合梁截面;
2 Astfst≥0.15Af的受负弯矩的组合梁截面。
|
